INTRODUCCIÓN::
Hasta ahora sólo hemos considerado límites de una función cuando x tiende a un número real a. Sin embargo, también podemos analizar el comportamiento de f(x), cuando x toma valores cada vez más y más grandes, sean estos positivos o negativos; es decir, cuando x → + ∞ (significa que “x” crece sin límite) o cuando x → - ∞ (significa “x” decrece sin límite). Esta clase de límites se denominan límites al infinito.
PROPIEDADES DE LOS LÍMITES :
Al evaluar límites al infinito, lo más seguro es que lleguemos a indeterminaciones matemáticas de la forma: ∞ / ∞, ∞ - ∞, 1∞, 0.∞, ∞0. Básicamente, trabajaremos las dos primeras.
Al evaluar el límite, debes tener en cuenta las propiedades de los límites que vimos en la tabla anterior y los siguientes dos TEOREMAS:
|
TEOREMA N° 1
|
TEOREMA N° 2, si n ∈ Z+
|
|
|
|
|
EN GENERAL
|
|
|
|
| INDETERMINACIONES MATEMÁTICAS DEL TIPO | |  |
Si al evaluar el límite una función racional del tipo f(x) = g(x) / h(x) por sustitución directa obtenemos una indeterminación del tipo ∞ / ∞ , para eliminarla seguimos los siguientes pasos:
PASOS:
1. Comprobar la indeterminación – Aplicamos sustitución directa.
2. Dividimos cada término por la mayor potencia de x
3. Operamos algebraicamente y simplificando los término semejantes.
4. Aplicamos las propiedades de los límites.
5. Expresamos simbólicamente el límite.
TEOREMA: Límite de una función polinómica.
El límite de una función polinómica en el infinito es + ∞ ó - ∞, dependiendo de que el coeficiente del término de mayor grado del polinomio sea positivo o negativo:
 | Si an en POSITIVO. |
 | Si an en NEGATIVO. |
EJEMPLO:
| Hallar el siguiente limite |  |
Es una función polinómica, el limite es +∞, ya que el signo del coeficiente de la mayor potencia (2) es POSITIVO.
EJEMPLO:
| Hallar el siguiente limite |  |
Es una función polinómica, el limite es - ∞, ya que el signo del coeficiente de la mayor potencia (-4) es NEGATIVO.
EJEMPLO N° 1:
| Hallar el límite de la siguiente función: |  |
PASO N° 1: Aplicamos sustitución directa
Debemos eliminamos la indeterminación matemática aplicando los pasos anteriores.
PASO N° 2: Dividimos cada término por la mayor potencia de x
PASO N° 3: Operamos algebraicamente y simplificando los término semejantes.
PASO N° 4: Aplicamos las propiedades de los límites.
PASO N° 5: Expresamos simbólicamente el límite.
| Hallemos |  | y |  | por medio de una tabla de valores, el ángulo “x” está dado en radianes. |
|
Ángulo x
|
-0.4
|
-0.3
|
-0.2
|
-0.1
|
0
|
0.1
|
0.2
|
0.3
|
0.4
|

|
0.97
|
0.98
|
0.99
|
0.998
|
1
|
0.998
|
0.99
|
0.98
|
0.97
|
Observa como los valores por derecha o izquierda, tienden a 1 (si realizas un procedimiento similar para la segunda situación, notaras que tiende a cero). Por lo tanto:
|
ALGUNAS IDENTIDADES
|
|
|
|
|  |
Para resolver límites de funciones trigonométricas, lo primero que debes hacer es evaluarlo. Si obtienes una indeterminación, ten en cuenta para eliminarla (si es posible) las siguientes recomendaciones:
RECOMENDACIONES
1. Sen 0 = 0 y Cos 0 = 1, quiere decir, que si x tiende a cero, Sen x no debe ser factor en un denominador.
2. Llevar la expresión a la forma de los límites trigonométricos básicos. Generalmente, multiplicando numerador y denominador por un mismo número o por la conjugada de uno de ellos.
3. Manejar con propiedad las principales identidades trigonométricas.
4. Manejar con propiedad los casos de factorización.
5. Dominar las operaciones y sus propiedades fundamentales.
6. Manejar con propiedad la reversibilidad de las operaciones.
7. Ir elaborando un listado de “artificios matemáticos” que encuentres durante el desarrollo de los ejercicios.
| EJEMPLO N° 1: Hallar el límite de la siguiente función |  |
PASO N°1: Aplicamos sustitución directa:
PASO N°2: Aplicamos las identidades Básicas:
PASO N°3: Expresamos simbólicamente el límite:
| EJEMPLO N° 2: Hallar el límite de la siguiente función |  |
PASO N°1: Aplicamos sustitución directa:
PASO N°2: Aplicando las identidades Básicas:
PASO N°3: Expresamos simbólicamente el límite:
EJERCICIOS PROPUESTOS










CONTINUIDAD
DEFINICIÓN:
En forma intuitiva podemos afirmar que una función es continua si su gráfica se puede trazar sin levantar el lápiz, sin interrupciones, es decir, en forma continua. Por el contrario, es discontinua, si trazamos su gráfica por etapas: primero un tramo y luego el otro, es decir, hay puntos o tramos donde la gráfica se interrumpe.
Consideremos las funciones:
Una función f(x) es continua en el punto x = a, si y sólo si se cumplen las siguientes tres condiciones:
|
1.
| | Si |  | existe |
|
2.
| | Si |  | existe |
|
3.
| | Si |  | Se cumple |
Para que una función sea continua debe cumplir las tres (3) condiciones anteriores, de no cumplir una sola de ellas la función es DISCONTINUA.
CONTINUIDAD EN UNA GRÁFICA
EJEMPLO N° 1
| Determinar gráficamente la continuidad de la función |
| en x = 1 |
 |
1
| f(1) = 1. |
|
2
|
|
|
|
|
|
3
|
|
La condición (1) y (2) se cumplen, por lo tanto f(x) es una función continua en x = 1. Decimos que la función representada en la Gráfica anterior es continua en x = 1.
EJEMPLO N° 2
| Determinar gráficamente la continuidad de la función |
| en x = -1 |
|
|
1
| f(-1) no existe, ya que x = -1 no tiene imagen, hay una asíntota vertical. |
|
2
|
|
|
|
|
|
3
| La condición (1) y (2) no se cumplen, por lo tanto f(x) no es una función continua en x = -1. |
Decimos que la función representada en la Gráfica anterior es discontinua en x = -1.
EJEMPLO N° 3
| Determinar gráficamente la continuidad de la función |
| en x = -1 |
|
|
1
| f(-1) = 1, Puesto que en x = -1, el intervalo es cerrado. |
|
2
|
|
|
|
|
|
3
| La condición (2) no se cumple, por lo tanto f(x) no es una función continua en x = -1., |
Decimos que la función representada en la Gráfica anterior es discontinua en x = -1.
EJEMPLO N° 4
| Determinar gráficamente la continuidad de la función |
| en x = 2 |
|
|
1
| f(2) = 1. Por definición. |
|
2
|
|
|
|
|
|
3
| La condición (2) no se cumplen, por lo tanto f(x) no es una función continua en x = 2. |
Decimos que la función representada en la Gráfica anterior es discontinua en x = -1.
DISCONTINUIDAD EVITABLE
Sea f(x) una función discontinua en x = a. Decimos que
f(x) posee una discontinuidad evitable o removible en
x = a
| si y sólo si |  | existe, en caso contrario la llamaremos discontinuidad inevitable o esencial. |
Como su nombre lo indica, la discontinuidad evitable es aquella que podemos obviar. Esto se logra simplemente
| haciendo que f(a) coincida con el |  | De esta manera lograremos que se cumplan dichas condiciones. |
|
En nuestras funciones, las gráficas 1 y 2 presentan discontinuidad evitable o removible, por tanto, la podemos obviar (volverlas continuas) con sólo redefinirlas. Veamos:
|
REDEFINIENDO N°1
|
REDEFINIENDO N°2
|
|
|
|
|
|
|
|
CONTINUIDAD ANALITICAMENTE
EJEMPLO N° 1
| Determinar la continuidad de la siguiente función en el punto x = -1 |  |
| PASO N° 2: Hallar límite lateral por la izquierda cuando x = -1 |  |
 | = |  |
| PASO N° 3: Hallar límite lateral por la derecha cuando x = -1 |  |
 | = |  |
| Como los límites laterales son iguales decimos que: |  |
| PASO N° 4: Comparamos f(a) y Lim f(x) |
|
Decimos que la función es continua en x = -1.
TEOREMA
1. Toda función polinomial es continua en cualquier punto, es decir, es continua en todo
R .
2. Cualquier función racional es continua siempre que esté definida; esto es, si es continua en su dominio.
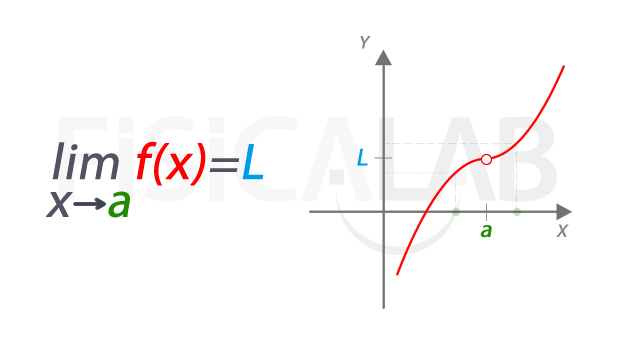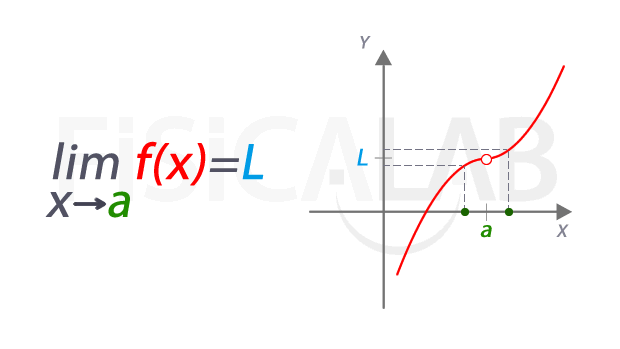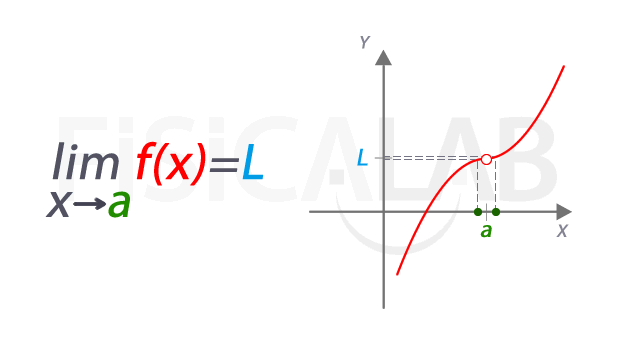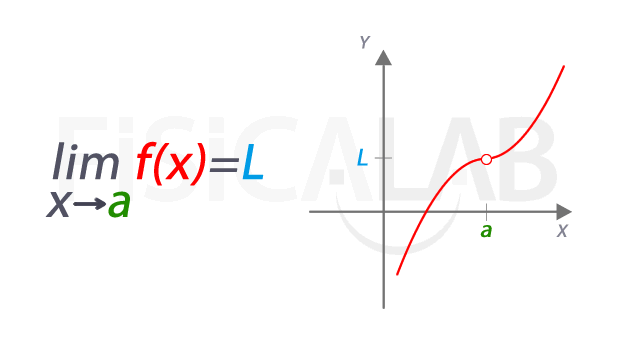

































































































































No hay comentarios.:
Publicar un comentario